热力学基础复习
基本定义
热力学第零定律
- 内容:如果两个物体都与处于确定状态的第三物体处于热平衡,则该两个物体彼此处于热平衡
- 宏观性质:处于同一热平衡状态的所有物体都具有共同的宏观性质,我们用温度来表征这一宏观性质
热力学过程
- 系统:在热力学中,把所研究的物体或物体组叫做热力学系统(thermodynamic system),简称系统(system)
- 准静态过程:准静态过程是无限缓慢的状态变化过程,在过程进行的每一 步确保系统的状态均可视为平衡态
- 热力学的研究是以准静态过程的研究为基础的
功 能量 内能
- 引入:
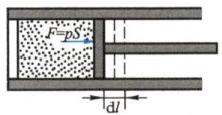
设有一气缸,其中气体的压强为p, 活塞的面积为S,活塞与气缸间无摩擦,为了维持气体时时处在平衡态,外界和气体对活塞的压力必须相等.当活塞缓慢移动一微小距离dl 时,在这一微小的变化过程中,可认为压强p 处处均匀且大小不变,在此过程中,气体所做的功为
$$
dA = pSdl = pdV
$$ - 式中dV 是气体体积的微小增量.在气体膨胀时, dV是正的,dA也是正的,表示系统对外做功;在气体被压缩时,dV 是负的,dA 也是负的,表示系统做负功,即外界对系统做功.
- 注意:这里的dA与我们高中定义的不同,反正我们高中说的是外界对气体做的功,也就是把对象调转了,注意区别
- 做功是系统与外界相互作用的一种方式,也是两者的能量交换的 一种方式.这种能量交换的方式是通过宏观的有规则运动(如机械运动、电流等) 来完成的.而热传递和做功不同,这种交换能量的方式是通过分子的无规则运动来完成
- 热力学系统具有一定的能量,叫做热力学系统的“内能”.上述实验事实表明:内能的改变量只决定于初末状态,而与所经历的过程无关.换句话说,内能是系统状态的单值函数.
热力学第一定律
如果有 一系统,外界对它传递的热量为Q, 系统从内能为E₁ 的初态改变到内能为E₂ 的 末态,同时系统对外做功为A, 那么,不论过程如何,总有
$$
Q = E_{2} - E_{1} + A\tag{6-2}
$$
上式的意义就是:外界对系统传递的热量,一部分使系统的内能增加,另一部分用于系统对外做功
热力学第一定律的应用
等容过程
等容过程的特征是气体的体积保持不变,即V为常量,dV=0,相应地,也就有dA = 0.,所以,外界传递给气体的热量全部用来增加气体的内能
摩尔定容热容:
- 定义:气体的摩尔定容热容,是指1 mol 气体在体积不变的条件下,温度改变1K(或1℃)所吸收或放出的热量,Cv,m表示,所以
$$
dE = \frac mM C_{v,m} dT \tag{6-7}
$$ - 应用:应该注意,上式是计算过程中理想气体内能变化的通用公式,不仅仅适用于等容过程!!!
- 计算:由上一章推导的内能公式
$$
E = \frac mM \frac i 2 R T
$$
两边微分之后与上式比较可得
$$
C_{v,m} = \frac i 2 R \tag{6-8}
$$ - 上式说明:理想气体的摩尔定容热容是一个只与分子的自由度有关的量,它与气体的温度无关
- 定义:气体的摩尔定容热容,是指1 mol 气体在体积不变的条件下,温度改变1K(或1℃)所吸收或放出的热量,Cv,m表示,所以
等压过程
注:以吸热膨胀为例
等压过程做的功(自己想象p-V图)
$$
A = p(V_{2}-V_{1})=\frac mM R (T_{2}-T_{1})\tag{6-10b}
$$吸热
$$
Q = \Delta E + A =E_{2}-E_{1} +\frac mM R (T_{2}-T_{1})\tag{6-11}
$$可见:气体在等压膨胀过程中,所吸收的热量一部分用来增加内能,另一部分用于气体对外做功;气体在等压压缩过程中,外界对气体做功,同时内能减小,放出 热量.
定义:我们把1 mol气体在压强不变的条件下,温度改变1K 所需要的热量叫做气 体的摩尔定压热容:
$$
C_{p,m} = \frac{\delta Q_{p}}{\frac mM dT}
$$计算:根据公式6-2,6-7以及6-11以及以上定义,可得迈耶公式
$$
C_{p,m} = C_{v,m}+R\tag{6-12}
$$理解:根据定义,等压过程所吸收的热量一部分用来增加内能,另一部分用于气体对外做功,而等容过程吸收的热量全部用来增加内能,所以摩尔定压热容大于摩尔定容热容也很好理解
摩尔热容比:由公式6-8和6-12可以得出
$$
C_{p,m}=\frac{i+2}2R \tag{6-13}
$$
我们把二者之比叫做摩尔热容比,用γ表示,该值只与气体分子的自由度有关, 而与气体温度无关.
$$
\gamma = \frac{C_{p,m}}{C_{v,m}}=\frac{i+2}i \tag{6-14}
$$
等温过程
特点:温度不变,内能不变
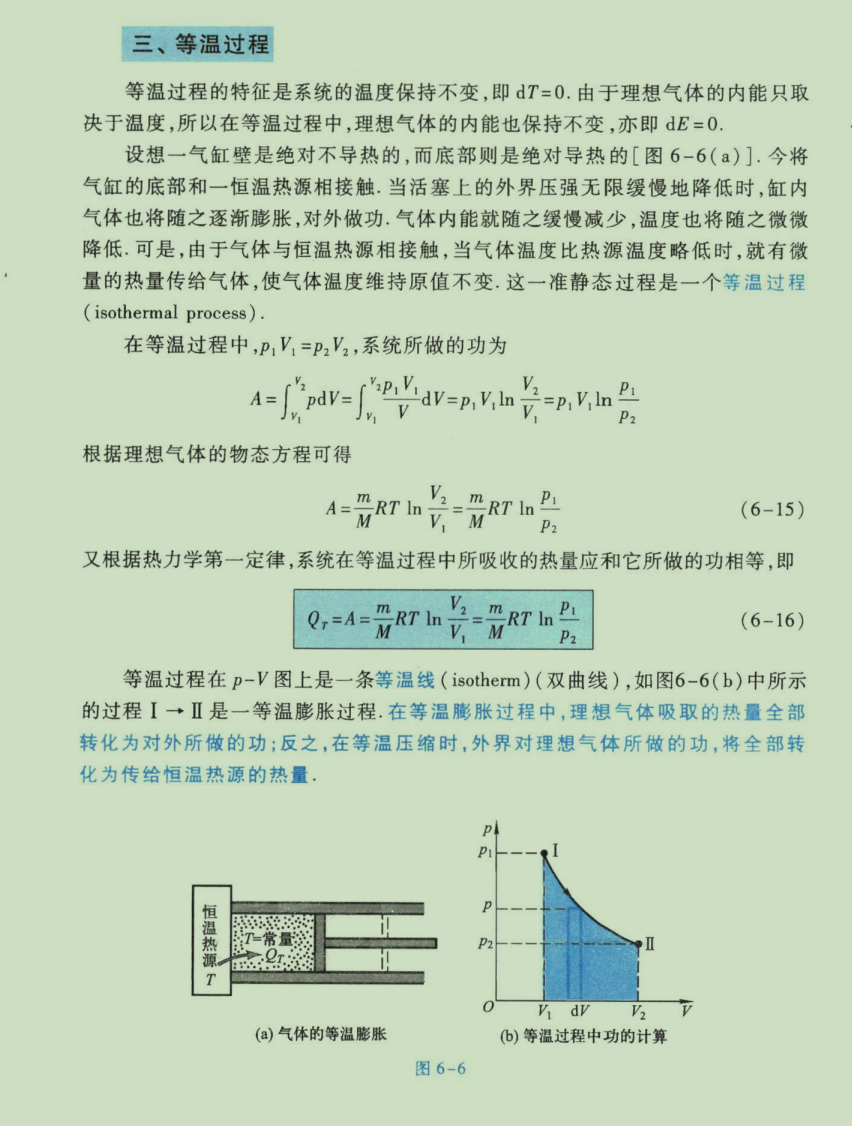
偷懒:由于书上只有一页介绍等温过程,而且比较精简,故直接附上图片(
其实是偷懒 😄)
绝热过程
