BUAA-OO-Unit1

这是2025年OO第一单元的总结博客

基于度量分析程序结构

类的设计考虑

先放一张类图

我采用了poly-Mono的核心结构，即将各因子、项、表达式都转化为多项式Poly，而多项式是由一个个的单项式Mono所构成，经过迭代之后，Mono的基本结构为
$$
Mono = ax^b\prod sin(Factor)^c*\prod cos(Factor)^d
$$
至于类的设计，我借鉴了OOpre hw7以及上机实验的框架，沿袭了Parser Lexer Expr Term以及诸多Factor类，然后根据归一化思想以及迭代需求，新增了DiyFunc NormalFunc Poly Mono TriFactor DeriveFactor 等类。

我将我所设计的类分为了几个package，处理过程大致如下：

首先是MainClass读入字符串，然后首先先将自定义函数分别放到Functions的DiyFunc和NormalFunc类进行处理，这是两个静态类，分别用于解析递归函数和普通函数，然后将解析后的函数存储在类自身的静态属性里面，后面可以直接通过类名进行调用，而无需实例化对象
然后读入要化简展开的表达式，首先调用Lexer进行词法分析，分析完毕后交给Parser进行处理，Parser采用递归下降法一层一层地解析表达式，从表达式到项再到因子
解析完表达式后，下面就要将各个因子所构成的项进行归一化，在每一个类里面都有一个toPoly()方法，用于将本类的对象转换为一个多项式
特别地，在转换求导因子时，我是直接将求导因子括号内的表达式转换为多项式，然后调用多项式的求导方法，将返回的多项式存储为这一个求导因子的属性
最后，遍历多项式的每一个单项式，打印输出

度量

类的复杂度

WMC 表示一个类中所有方法的复杂度之和。通常，每个方法的复杂度用 圈复杂度 (Cyclomatic Complexity) 来衡量，WMC 越高，类的复杂度越高，维护和测试的难度也越大
OCavg 反映了类中方法的平均复杂度，如果 OCavg 较高，说明类中的方法普遍较复杂，可能需要重构。
OCmax 反映了类中最复杂方法的复杂度，如果 OCmax 过高，说明类中可能存在过于复杂的方法，需要重点关注和重构

![](../img_post/2025-03-22 152021.png)

分析结果可知，DiyFunc类、Lexer类和Parser类复杂度较高，为低内聚类。这三个类分别为递归函数类、词法分析类和递归下降执行类，均为程序运行流程的直接体现，因此它们作为低内聚类是可以理解的。同时，其它类耦合度低，可以认为整份代码的抽象化程度还算比较合适。当然，我的DiyFunc类还是比较“笨重”的，因为对于一个参数和两个参数的递归函数，我并没有将其统一起来，而是设计了两个方法，recurrence1和recurrence2，这样的设计无疑是不太好的，但是我刚开始写的时候怕出错，也就分开设计了，后面也没有整改🫠。其实还是有改进空间的。

方法的复杂度

这里选了复杂度的前几位

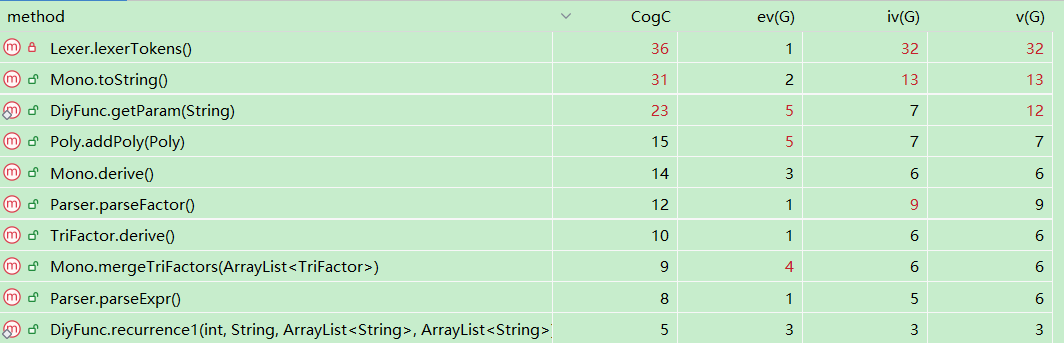
其中，Lexer在解析输入时，有非常非常多的分支判断，因此复杂度异常地高，这也是合理的。

然后Mono的toString方法是将单项式转换为字符串，这里面牵扯到三角函数嵌套表达式的诸多问题，因此复杂度也比较高

代码行数

![](../img_post/2025-03-22 151812.png)

三次迭代下来，总共大概1000行代码，应该还算少的了，因为本人对于卷性能卷优化不太感冒，而且很多地方追求精简，所以代码量少了些

架构设计体验

本人架构倒是还行，至少没经历过重构，但是依旧bug多多🫠

第一次迭代

本人在浏览了一些学长博客和实验代码后，果断选择了递归下降法+Poly-Mono结构，即最后的整个式子是一个多项式Poly,它有若干个单项式Mono相加减组成，在第一次迭代中
$$
Mono = a*x^b
$$

第二次迭代

第二次迭代引入了三角函数因子和自定义递归函数这两个新特性，难度可谓是直线上升，思考良久后，我发现，依旧可以将其统一为Poly-Mono结构，只是Mono的结构复杂了一些
$$
Mono = ax^b\prod sin(Factor)^c\prod cos(Factor)^d
$$
表现在代码上就是Mono类多了一个属性，那就是private ArrayList<TriFactor> triFactors = new ArrayList<>()，因此，合并同类项时也带来了极大的麻烦，两个单项式可以合并的条件变得异常复杂，需要对应的三角函数的值相等，而怎么判断值相等呢？比如2x^3 * sin(x+1) 和 3*x^3 * sin(1+x)，那么又需要设置三角函数的类的值相等的判断方法，但三角函数括号里可能是任何表达式或者因子，因此理论上也需要递归下降判断，但是我是直接带调用了toString方法再加上sort方法，判断字符串是否相等，对于大部分简单的情况还是能够拿捏的😁

第三次迭代

第三次增加了普通函数和求导因子，普通函数的各种思想和方法在递归函数里已经实现了，问题不大，求导因子的话我是选择在Poly和Mono里求导，这里需要注意的是，Mono求导返回的应该是一个Poly，然后根据乘法法则和链式法则求导即可，还要写一下三角函数的求导。这样设计的好处是只需要在三个类里面写求导方法，而不是每一层结构和每一种因子都要写，比较简洁。

自己的bug

第一次迭代

是的，我第一次都有bug，大致就是这样😰

第二次迭代

这次迭代直接就爆了

首先是我在第一次迭代中，实现了把符号直接读入数字中，比如指数的数字以及乘号后面的数字，因此我解析到的符号都是运算符，但是第二次有函数调用，f()括号里的数字如果有符号，那么我就会解析错，属于是没考虑到吧，也或许是第一次这样设计的不太合理，第一次的设计如下：

else if (expr.charAt(pos) == '+') {
                if (pos > 1 && (expr.charAt(pos - 1) == '^' || expr.charAt(pos - 1) == '*')) {
                    pos++;
                    parseNumber(1);
                }
                else {
                    tokens.add(new Token(Token.Type.OP, "+"));
                    pos++;
                }
            }
            else if (expr.charAt(pos) == '-') {
                if (pos > 1 && expr.charAt(pos - 1) == '*') {
                    pos++;
                    parseNumber(-1);
                }
                else {
                    tokens.add(new Token(Token.Type.OP, "-"));
                    pos++;
                }
            }

还有一个大的bug是我递归函数代入参数时，直接先后代入的，如果第一个实参里有第二个形参，那么也会被替换，修改后如下：

1 2	`return func.replace(formPara1, "$0").replace(formPara2, "$1") .replace("$0", "(" + para1 + ")").replace("$1", "(" + para2 + ")");`

第三次迭代

主要就一个，感谢zhench的评测机测出来了，就是第二次我是用逗号切割的函数参数，但是第三次迭代，函数调用里还可能有函数调用，因此不能直接盲目用逗号切割，需要考虑括号层数

发现别人程序bug

主要就是用自己踩过的一些坑来测试别人的代码
构造一些卡时间或者内存的样例，来测试一些实现不够敏捷的代码

这里不得不小小吐槽一下：感觉课程组的cost卡的很严，很多的数据其实开销并不算大，但是就是刀不了人，感觉这方面卡的太严了，互测的体验很糟糕，最后不得已交了一些001这样的水数据上去

优化

个人并未做过度的优化，仅仅是在输出时，指数为0,1,系数为0，+-1的特殊情况简化了一下输出，看起来更加舒适，至于过度的卷性能，卷二倍角公式、和差化积公式等，我个人并不感冒，也不觉得有多么高大尚

心得体会

Unit1还是压力很大的，至少我是感到比较吃力的，尤其是第二次迭代，让多少朋友们周五半夜，周六白天还在奋战。当然，可能课程组看我们上学期基本都学了oopre，所以加了些难度吧🫠
第一次最开始感觉无从下手，后面果断开始写，边写拜年思考，后面也就明悟了；但是第二次迭代感觉难度一下上去了，三角函数的引入让合并同类项出现许多难题，递归函数也是很棘手的，最后强测结果也有不少人直接寄掉，比如我；然后第三次迭代，感觉又太容易了一点儿，三下五除二就解决了。所以，这样的难度梯度设计是否合理，还是值得思考的🤔
说归说，还是很感谢课程组的，还是很感谢Unit1的，无论是递归下降法的精妙还是架构设计的经验，都让我受益良多，也锻炼了我的debug能力和抗压能力。递归下降法的精妙或许编译原理课程我们还会感受到