李宏毅机器学习-类神经网络训练
这是我学习机器学习时记录的一些笔记 ,希望能对你有所帮助😊
Some Terms
Critical Point
在深度学习中,“critical point”(关键点/临界点)指的是损失函数曲面(loss landscape)上梯度为零的点。数学上,这意味着损失函数L(通常是关于模型参数θ的函数)的梯度(或一阶导数)∇L(θ)等于零向量:∇L(θ) = 0
然而,并非所有的关键点都是我们想要的全局最小值(Global Minimum)。关键点可以分为几类:
局部极小值点(Local Minima):
- 在该点的某个局部邻域内,损失函数的值是所有点中最小的(但可能比全局最小值要大)。
- 这是优化过程中比较理想的点,虽然不是全局最优,但可能是足够好的解。
- 特点: 在局部最低点,类似于山谷底部。
局部极大值点(Local Maxima):
- 在该点的某个局部邻域内,损失函数的值是所有点中最大的。
- 在最小化损失函数的问题中(几乎所有深度学习任务都是),极大值点是我们想要避开的点。
- 特点: 在局部最高点,类似于山顶(但损失高,性能差)。
- 在深度学习中的现实性: 由于神经网络通常具有非常高的维度(参数众多),且损失函数通常无界向上,局部极大值点在深度学习的高维空间中极其罕见。更常见的是“反”方向的——鞍点。
鞍点(Saddle Points):
- 这是深度学习中最普遍、也最具挑战性的关键点类型。
- 该点不是局部极小值点也不是局部极大值点。
- 在通过该点的某些方向上,损失函数上升;在另一些方向上,损失函数下降。
- 特点: 形状类似于马鞍——在某些方向是“谷底”,在某些方向是“山顶”。
- 在高维空间中的普遍性: 随着模型参数维度的增加(这正是深度神经网络的特点),损失函数曲面的鞍点数量会指数级地多于局部极小值点。研究表明,在深度学习中,阻碍训练收敛的主要障碍物更可能是鞍点而不是局部极小值。
- 影响: 在鞍点处,梯度为零,标准的优化算法可能会停滞不前。如果下降方向“被困”在鞍点的平坦区域或上升方向,损失很长时间不会下降,学习变得非常缓慢,类似于“高原现象”。但在正确的方向上,损失是可以继续下降的。
如何应对关键点(尤其是鞍点)?
- 使用带动量(Momentum)的优化器: 如SGD with Momentum, Adam, RMSProp等。动量可以帮助参数更新“冲过”鞍点中平坦或轻微上升的区域,因为它积累了之前梯度的方向。
- 自适应学习率: 像Adam这样的优化器会调整每个参数的学习率,有助于更快地逃离鞍点沿着下降方向前进。
- 批归一化(Batch Normalization)等技巧: 通过平滑损失函数曲面,可能有助于减少鞍点带来的影响。
- 合适的初始化: 好的参数初始化策略(如Xavier, He Init)可以让网络从更容易优化的位置开始。
- 随机性: SGD本身固有的随机性(基于小批量样本计算梯度)有助于逃离某些鞍点。
Batch Size
- Smaller batch requires longer time for one epoch
- Smaller batch size has better performance
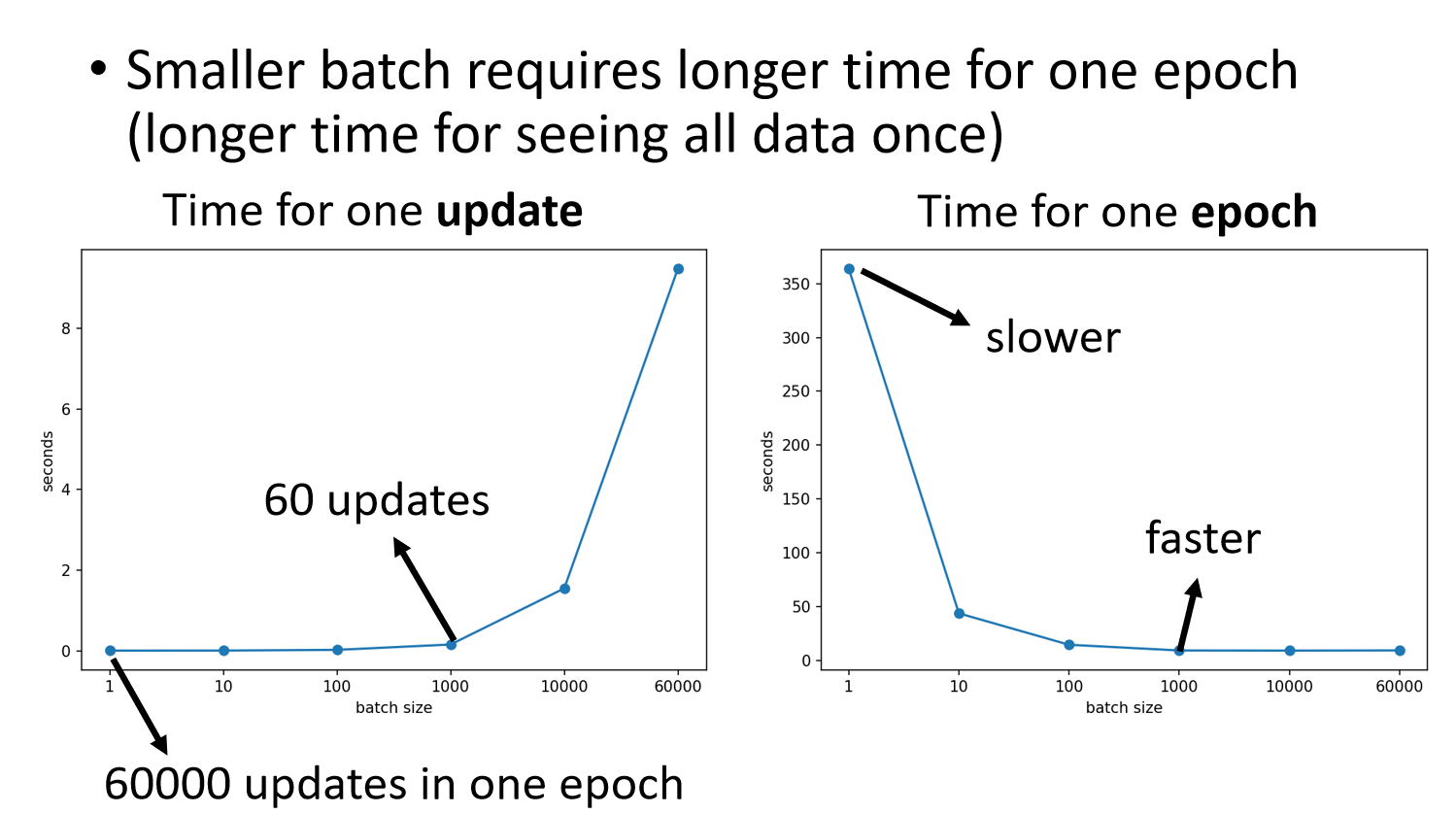
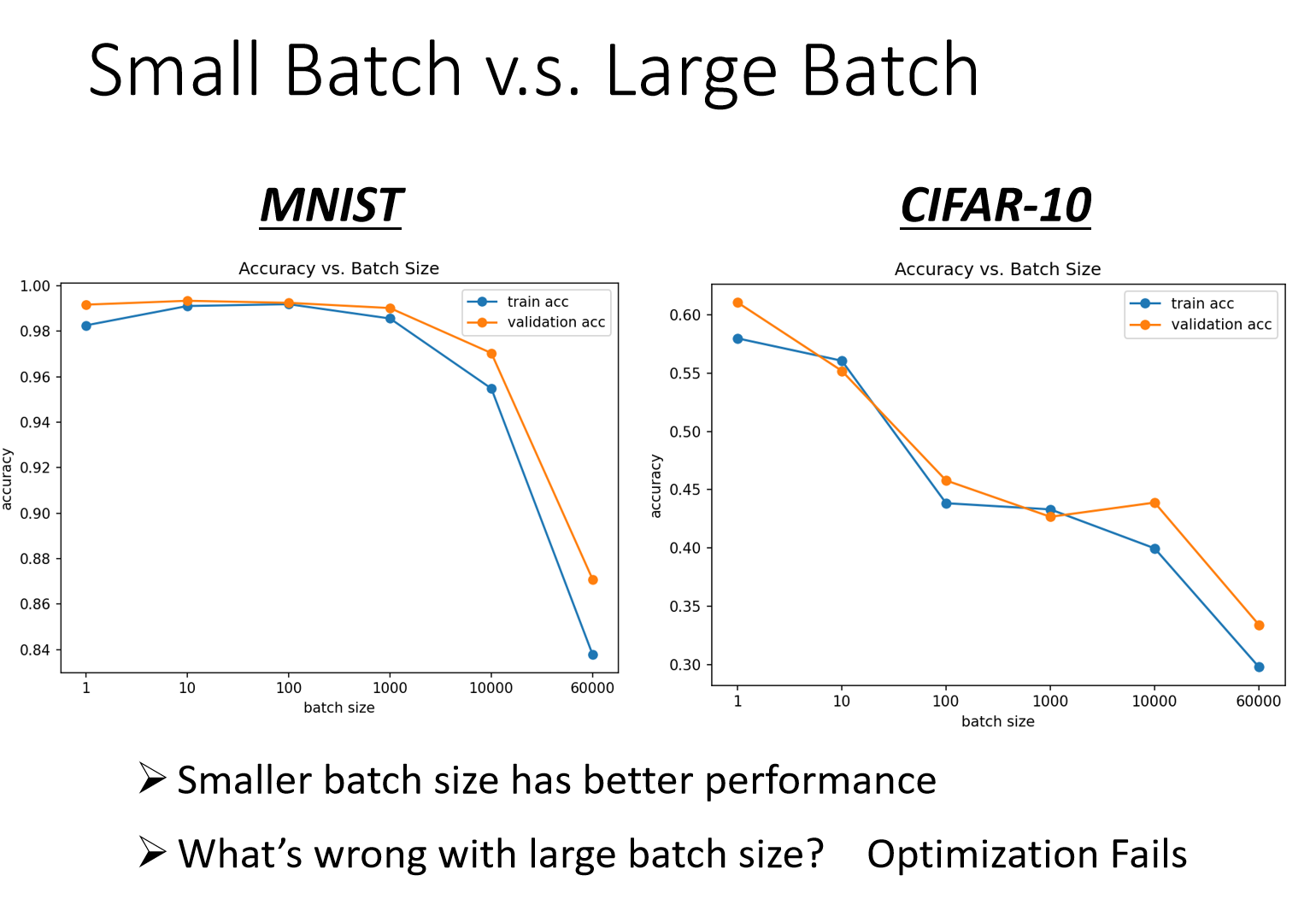
Better Optimization
Momentum
Momentum introduces a weighted sum of previous gradients to accelerate gradient descent. The movement is defined as the movement of the last step minus the gradient at the present step. The process is as follows:
$$
\begin{align}
m^0 &= 0 \
m^1 &= -\eta g^0 \
m^2 &= \lambda m^1 - \eta g^1 \
&\vdots \
\theta^{t+1} &= \theta^t + m^t
\end{align}
$$
where:
$m^t$ is the movement at step,
$\lambda$ is the momentum coefficient (0 < $\lambda$ < 1),
$\eta$ is the learning rate,
$g^t$ is the gradient at step.
This method ensures the movement is not just based on the current gradient but also on the previous movement, improving convergence.
Adaptive Learning rate
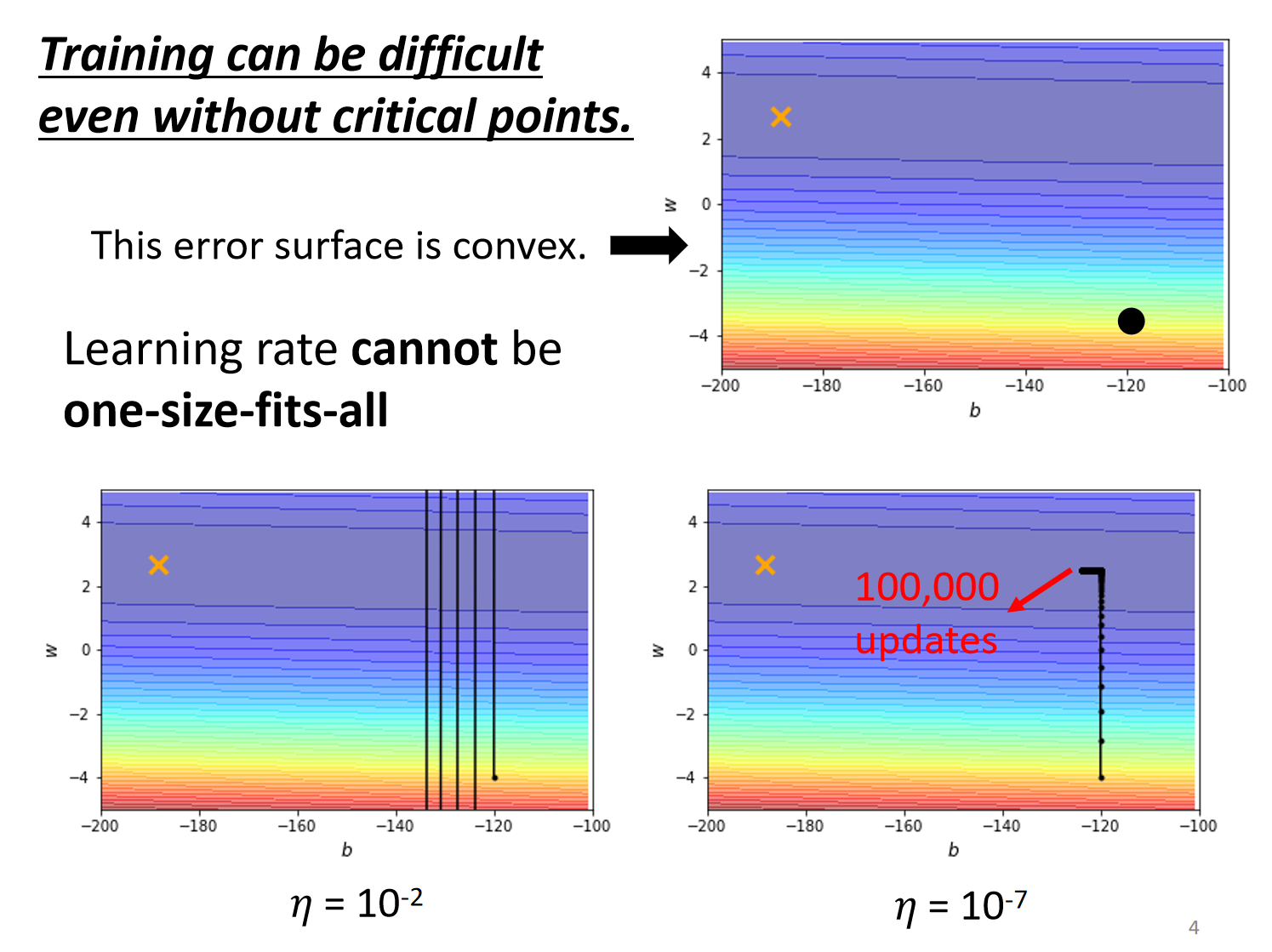
所以我们需要修改Optimization的公式,由公式1替换为公式2,$σ_i^t$ 是一个与时间、特征都有关系的量。
$$
\begin{align}
θ_i^{t+1}←θ_i^t−ηg_i^t \
θ_i^{t+1}←θ_i^t−\frac η{σ_i^t}g_i^t \
\end{align}
$$
具体的更新过程可以有几种方式
RMS
$$
\begin{align}
θ_i^1&←θ_i^0−\frac η{σ_i^0}g_i^0 & σ_i^0&=\sqrt{(g_i^0)^2} = |g_i^0| \
θ_i^2&←θ_i^1−\frac η{σ_i^1}g_i^1 & σ_i^1&=\sqrt{\frac1 2(g_i^1)^2 + (g_i^0)^2} \
θ_i^3&←θ_i^2−\frac η{σ_i^2}g_i^2 & σ_i^2&=\sqrt{\frac1 3(g_i^2)^2 + (g_i^1)^2 + (g_i^0)^2} \
\vdots &&& \
\end{align}
$$
但是RMS的问题是所有的梯度具有一样的权重,优化过程中,不同时间步的梯度可能差异极大(例如某些参数梯度大,某些梯度小),静态 RMS 无法自适应调整学习率,也就是无法敏锐捕捉当前梯度的变化趋势,可能造成震荡。因此诞生了RMS Prop
RMS Prop
自适应调整
$$
\begin{align}
\theta_i^1 &\leftarrow \theta_i^0 - \frac{\eta}{\sigma_i^0} g_i^0 & \sigma_i^0 &= \sqrt{(g_i^0)^2} \quad 0 < \alpha < 1 \
\theta_i^2 &\leftarrow \theta_i^1 - \frac{\eta}{\sigma_i^1} g_i^1 & \sigma_i^1 &= \sqrt{\alpha (\sigma_i^0)^2 + (1 - \alpha) (g_i^1)^2} \
\theta_i^3 &\leftarrow \theta_i^2 - \frac{\eta}{\sigma_i^2} g_i^2 & \sigma_i^2 &= \sqrt{\alpha (\sigma_i^1)^2 + (1 - \alpha) (g_i^2)^2} \
\vdots &&& \
\theta_i^{t+1} &\leftarrow \theta_i^t - \frac{\eta}{\sigma_i^t} g_i^t & \sigma_i^t &= \sqrt{\alpha (\sigma_i^{t-1})^2 + (1 - \alpha) (g_i^t)^2}
\end{align}
$$
Adam
Adam: RMSProp + Momentum
值得一提的是,RMSProp 和 Momentum 都涉及到了历史梯度,是否重复呢?非也
因为RMS计算的是一个平凡根,是一个scalar
而Momentum则是前一步移动的向量相加,不仅会有大小还会有方向上的影响。
Learning Rate Scheduling
将参数$\eta$也随时间改变,变化的方式有两种
$$
\begin{align}
\eta&\leftarrow\eta^t \ \theta_i^{t+1} &\leftarrow \theta_i^t - \frac{\eta^t}{\sigma_i^t} g_i^t
\end{align}
$$
Decay
Warm up
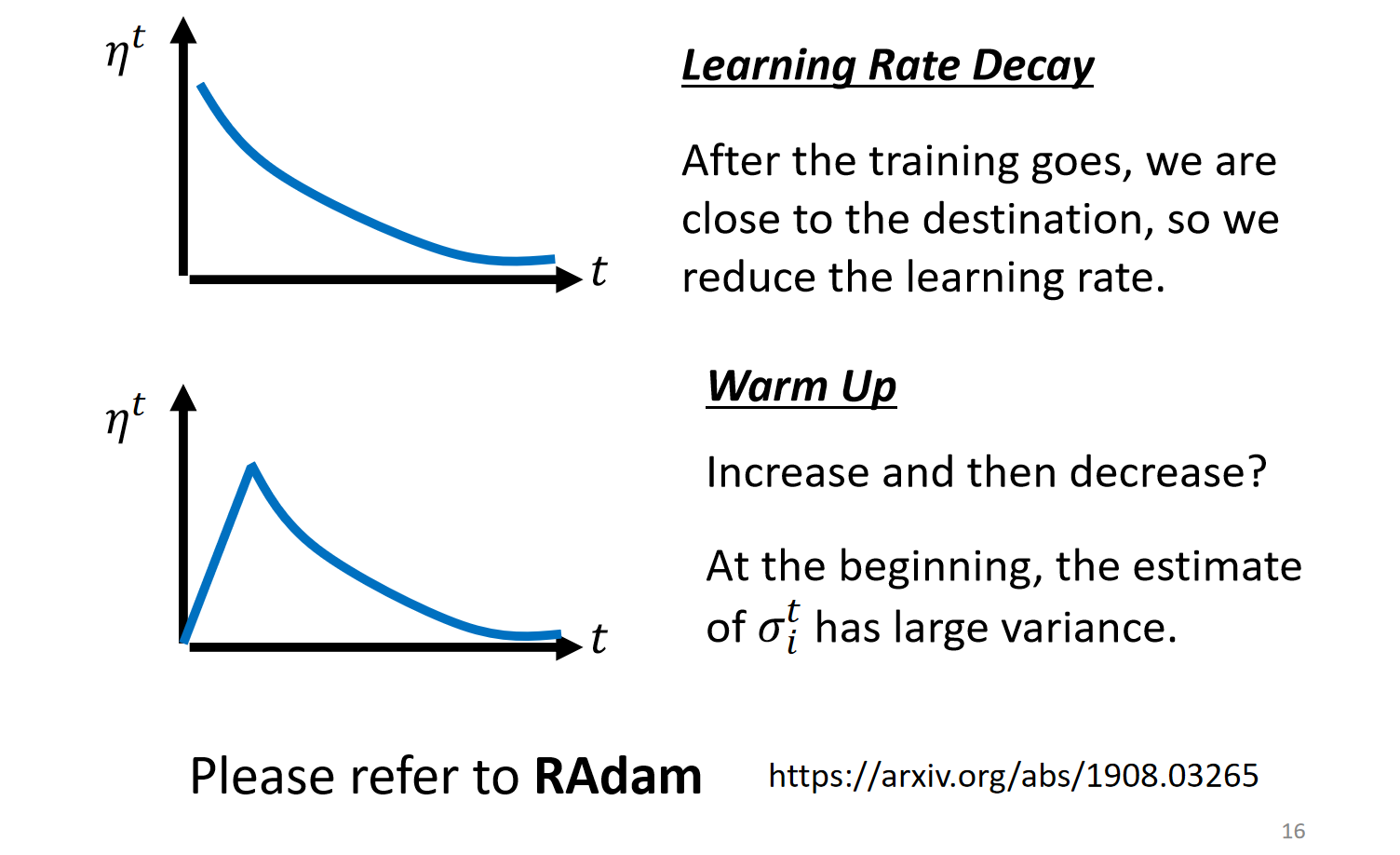
Batch Normalization
引入
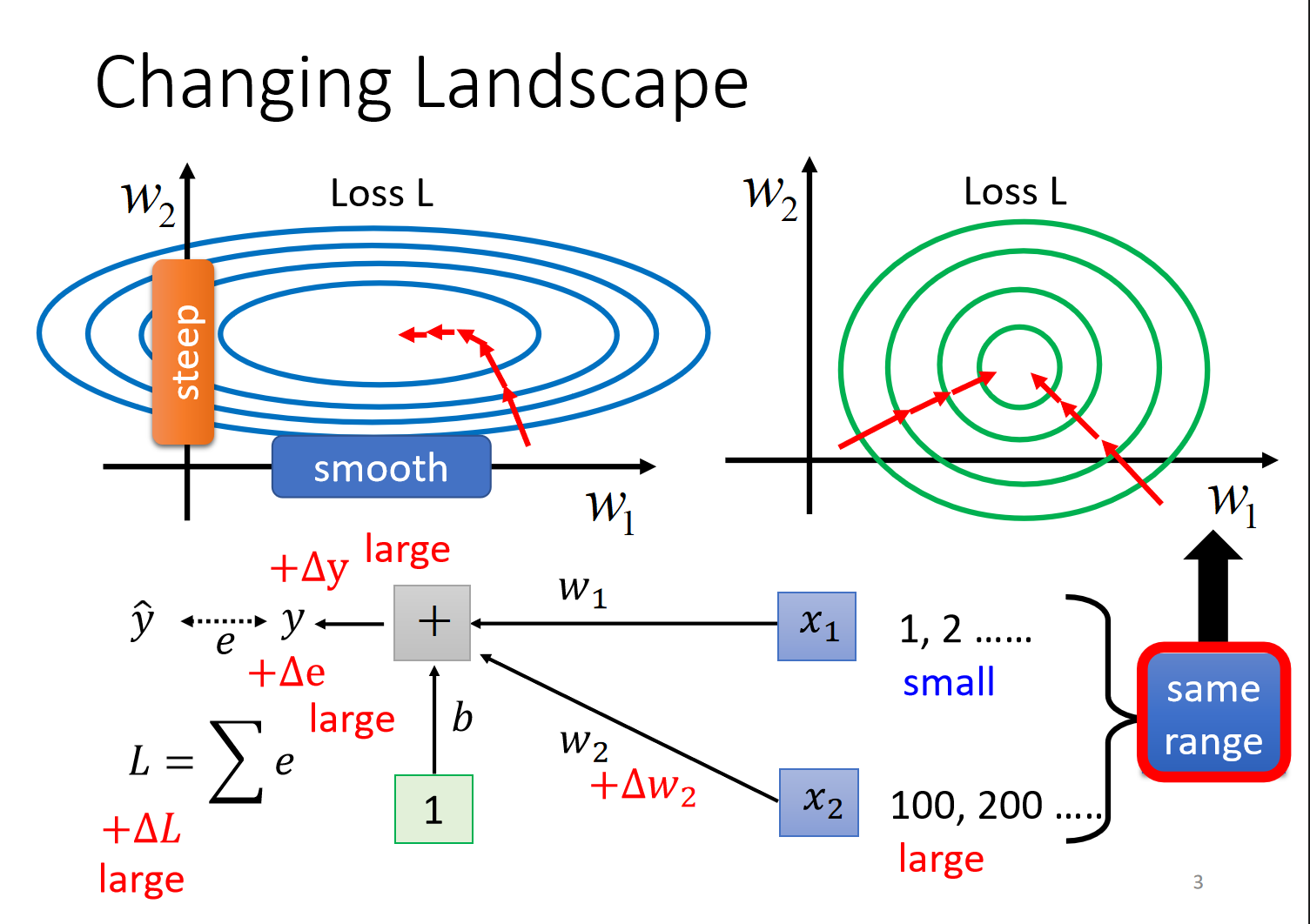
- 当不同feature的分布与值大小差别很大时,不同的weights 变化程度差异大,导致
error surface比较崎岖,难以训练、收敛,因此需要将数据归一化