Diffusion-原理解析
这是我学习Diffusion时记录的一些笔记 ,希望能对你有所帮助😊
基本概念
Diffusion Model(扩散模型)包含两个核心过程:
前向过程 (Forward Process): 这是一个固定的过程。它在 $T$ 个时间步内,逐步地向一个清晰的原始图像 $x_0$ 中添加高斯噪声,直到图像在 $T$ 时刻变为一个纯粹的随机噪声 $x_T$。
反向过程 (Reverse Process): 这是一个可学习的过程。模型从纯粹的噪声 $x_T$ 开始,通过一个神经网络(通常是
U-Net)在 $T$ 个时间步内逐步去噪,最终重建出清晰的图像 $x_0$。
与 VAE (Variational Autoencoder) 相比,VAE 试图通过 Encoder 将图像压缩到一个潜在向量,再通过 Decoder 重建,而 Diffusion Model 则是将这个过程分解为 N 个“加噪”和“去噪”的步骤。
Framework
Overview
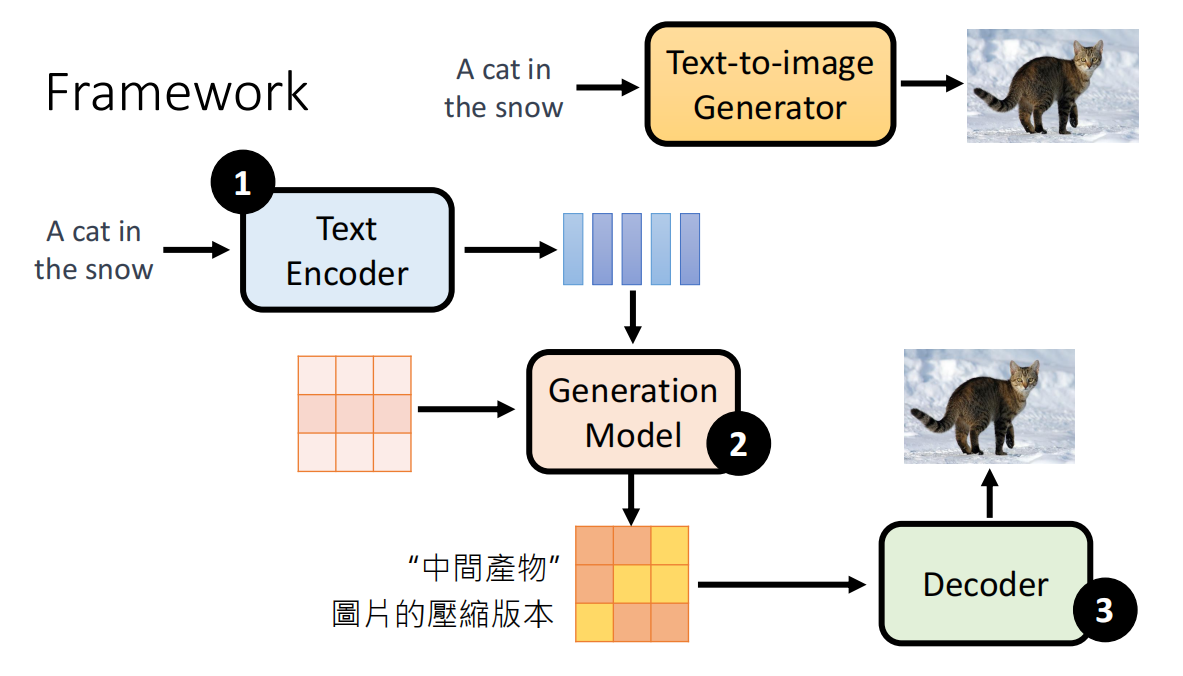
- 内部大致是三个模块,分别进行训练
Examples
- Stable Diffusion、DALL-E、Imagen 的架构类似
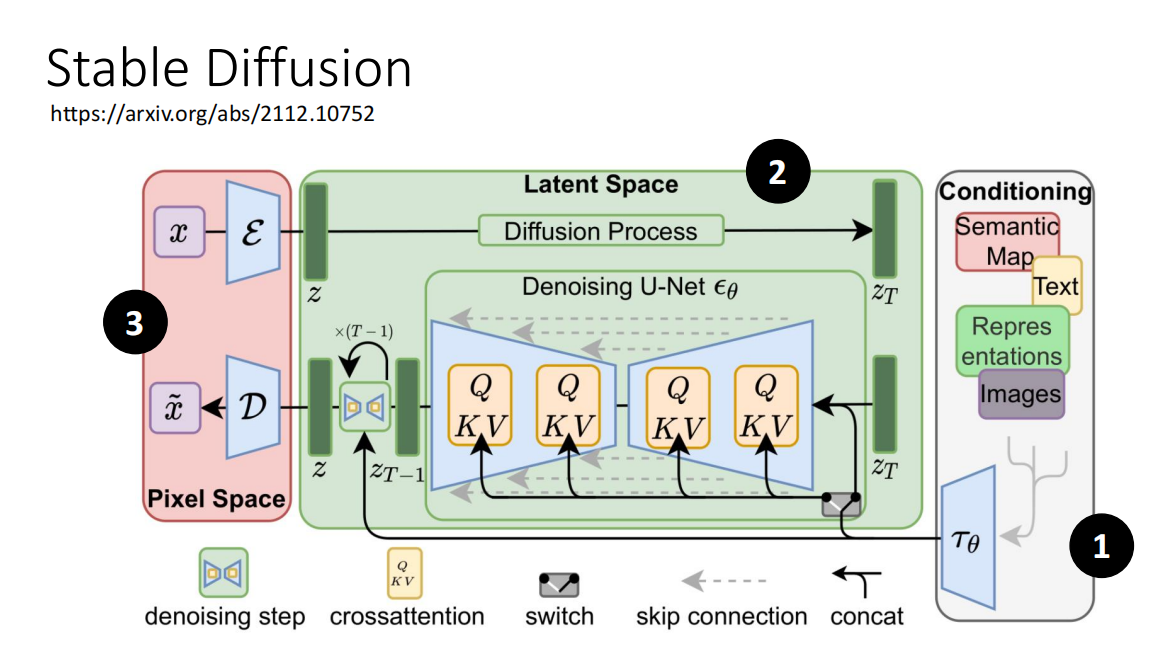
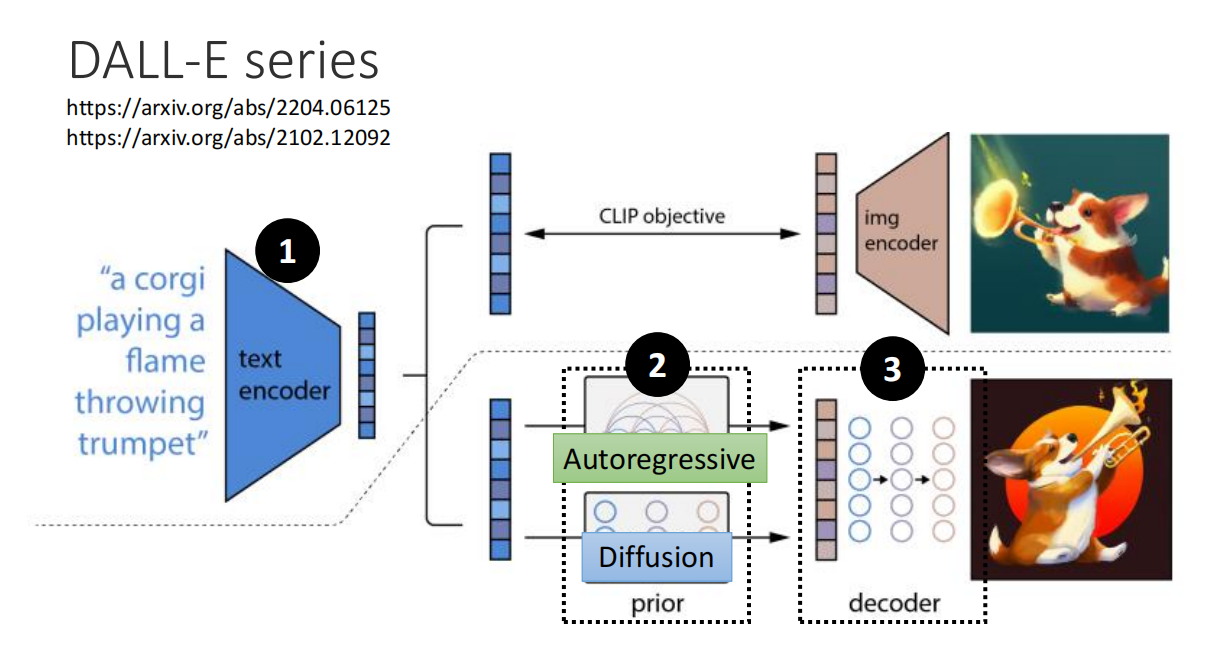
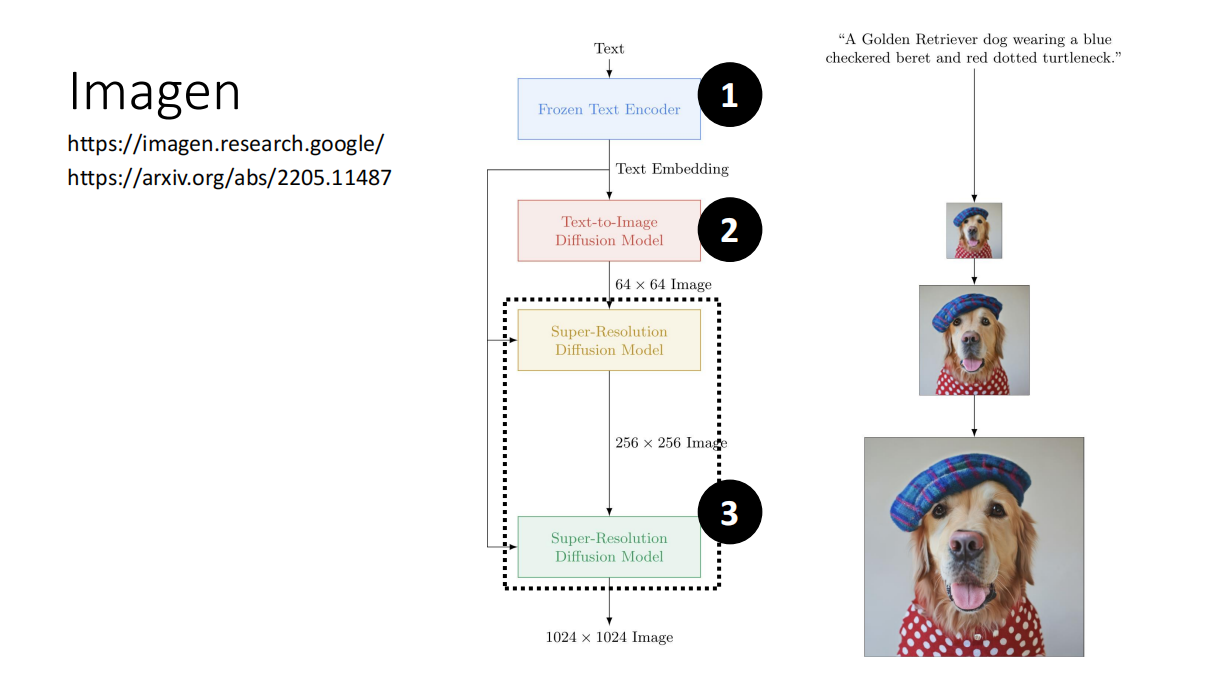
- 其实可以发现,第三个Decoder 就是一个超分模块,将低像素的模糊图片转换为清晰的图片
组成
1、Text Encoder
FID
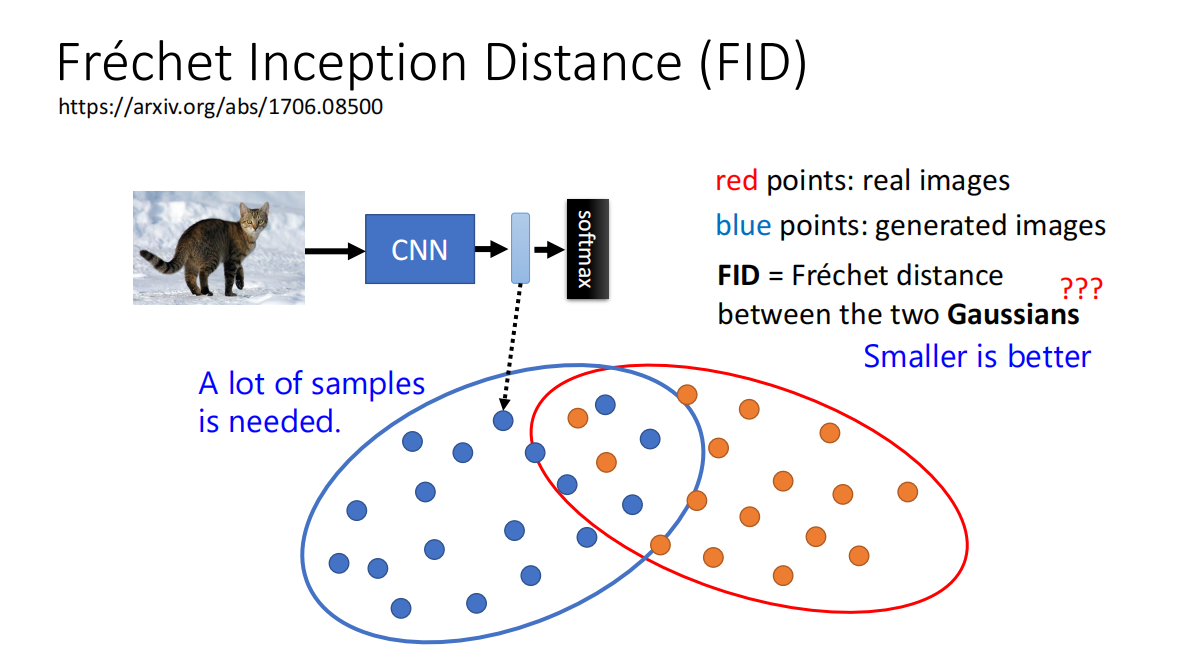
FID用来衡量生成的图片的质量- 将真实图片与生成图片的
latent space的分布视为Gaussian Distribution,然后计算两个Gaussian Distribution之间的距离
重要性
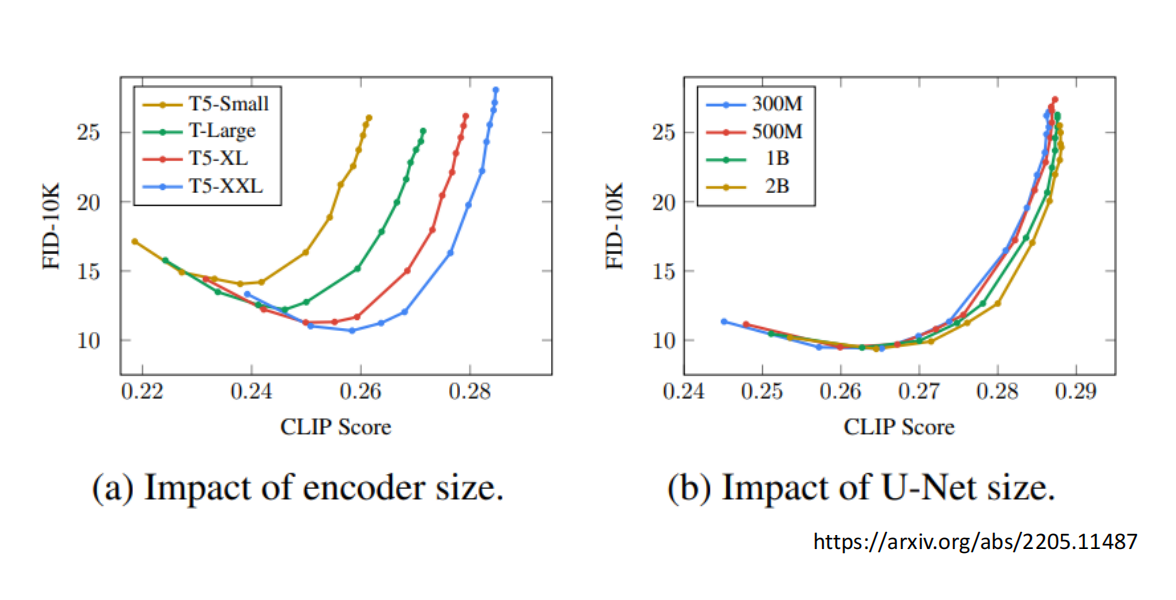
- 由图观察可知,
encoder的大小 质量 对最后生成的图片的质量影响更大,相比之下,U-Net 也就是Generation Model的影响没那么显著
CLIP
- Contrastive Language-Image Pre-Training
- 在 400 million image-text pairs 上训练
- 具备通用的图文理解能力
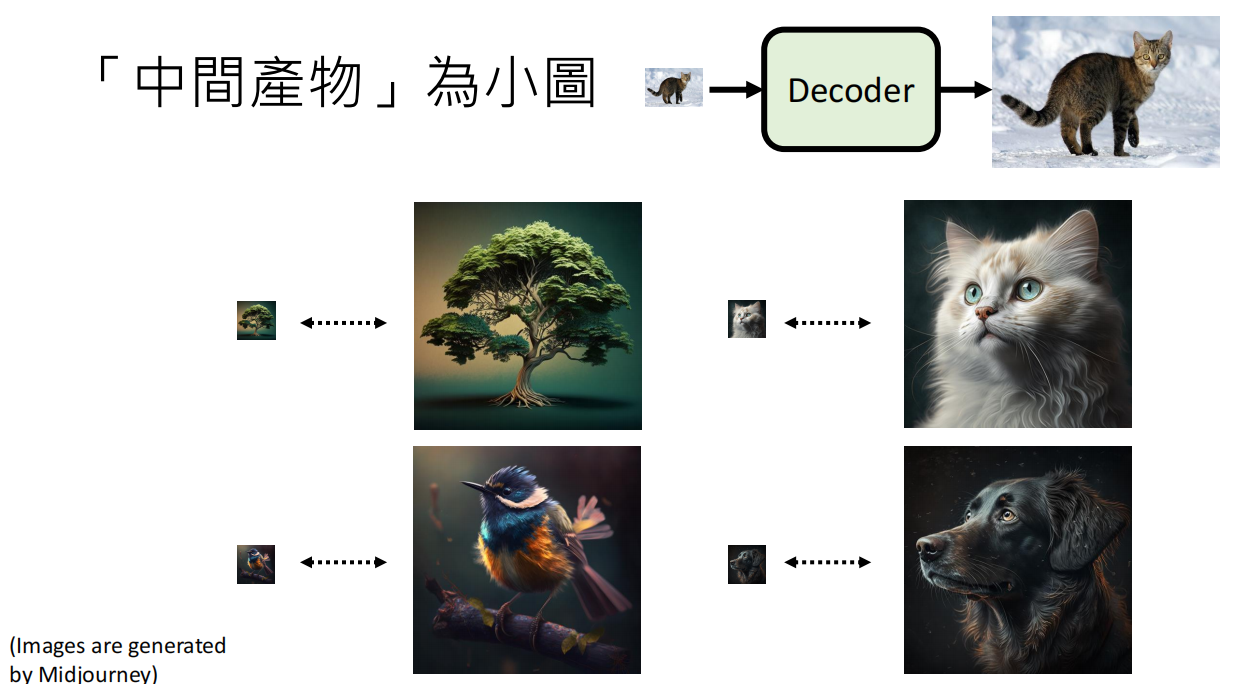
2、Decoder
- Decoder can be trainedwithout labelled data.
- 其实是一个超分模块
- 可以将原始图片通过一个Encoder 变小后 再用来训练 Decoder
- Latent Representation
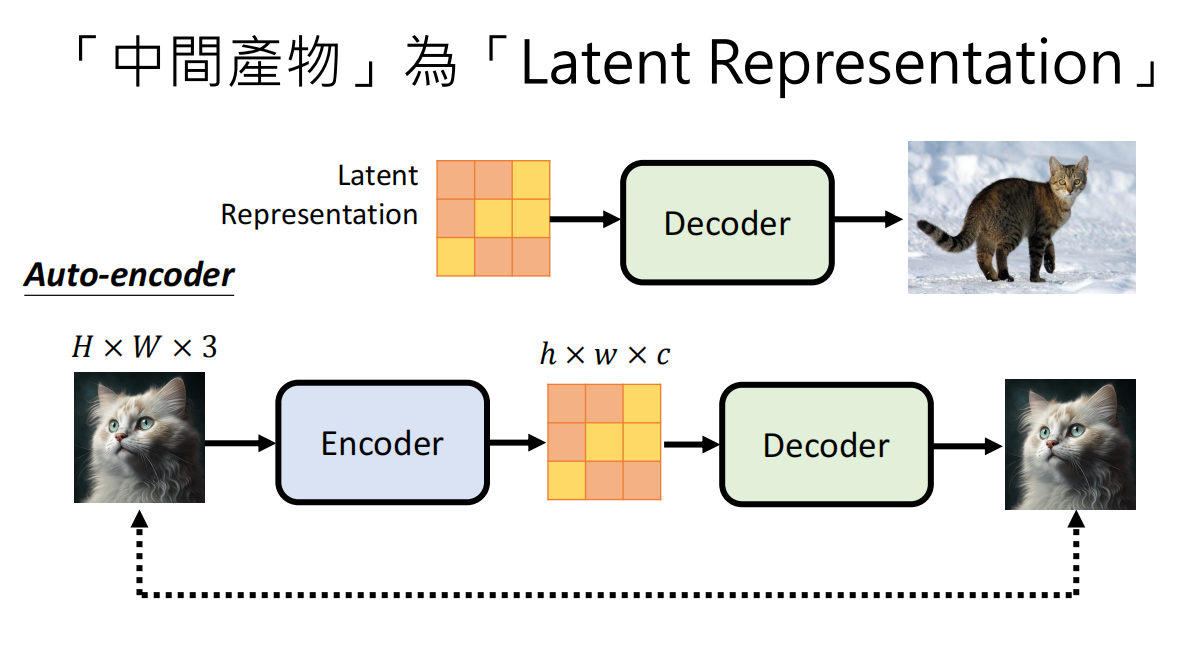
3、Generation
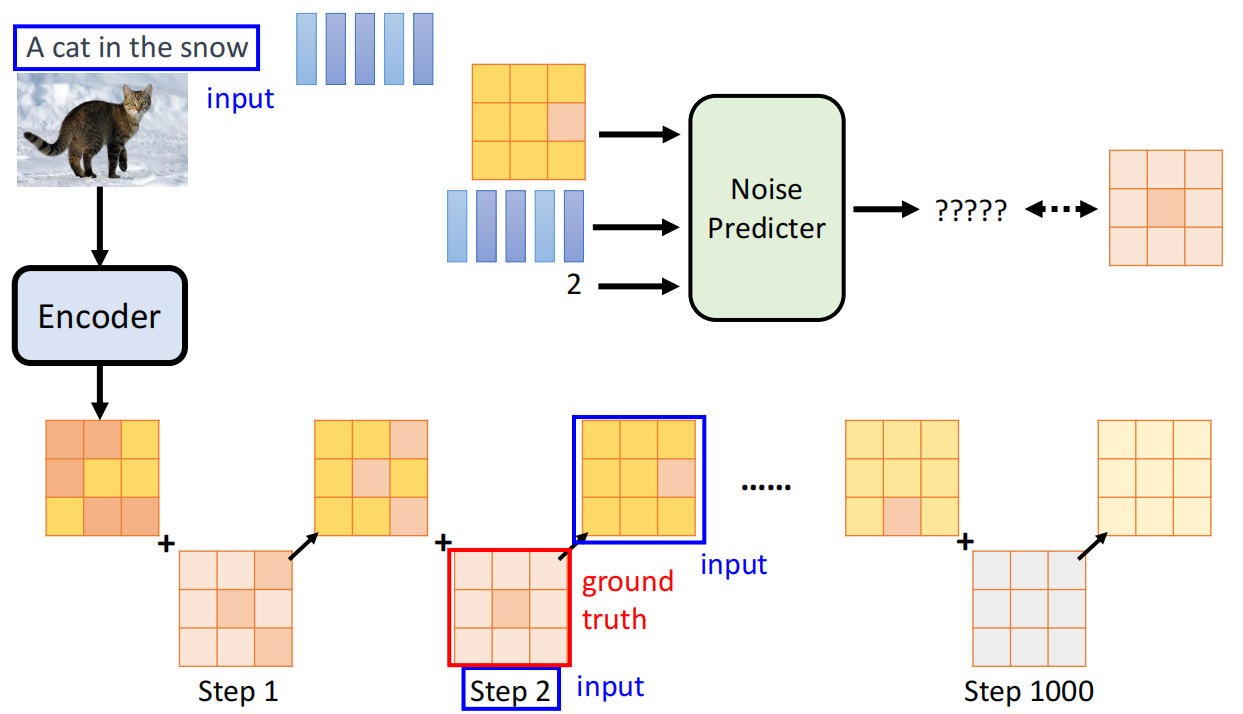
核心算法 (DDPM)
- 重点介绍DDPM (Denoising Diffusion Probabilistic Models) 的两个核心算法:

算法 1:训练 (Training)
训练的目标是让神经网络学会“预测噪声”。
- 从数据集中随机采样一个清晰的图像 $x_0$。
- 随机选择一个时间步 $t$(从 $1$ 到 $T$)。
- 随机采样一个与 $x_0$ 同样大小的标准高斯噪声 $\epsilon$。
- 关键步骤: 使用一个“捷径”公式(前向过程的数学技巧),直接根据 $x_0$, $t$, $\epsilon$ 生成在 $t$ 时刻的带噪图像 $x_t$:
$$
x_t = \sqrt{\overline{\alpha}{t}}x{0}+\sqrt{1-\overline{\alpha}_{t}}\epsilon
$$ - 将 $x_t$ 和时间步 $t$ 一起输入到噪声预测网络 $\epsilon_{\theta}$ 中,得到网络预测的噪声 $\epsilon_{\theta}(x_t, t)$。
- 计算网络预测的噪声 $\epsilon_{\theta}$ 与步骤 3 中采样的真实噪声 $\epsilon$ 之间的均方误差 (MSE) 损失。
- 通过梯度下降更新网络参数 $\theta$ 来最小化这个损失。
训练目标(损失函数):
$$
\nabla_{\theta}||\epsilon-\epsilon_{\theta}(\sqrt{\overline{\alpha}{t}}x{0}+\sqrt{1-\overline{\alpha}_{t}}\epsilon,t)||^{2}
$$
简单来说,就是训练一个网络,让它在给定 $t$ 时刻的带噪图像 $x_t$ 时,能准确预测出当初添加的噪声 $\epsilon$。
算法 2:采样 (Sampling / Inference)
在采样(即生成图像)阶段,我们执行“反向过程”。
从一个标准高斯分布中采样一个纯噪声图像,作为 $x_T$。
从 $t=T$ 开始,循环递减到 $t=1$:
a. 将当前的带噪图像 $x_t$ 和时间步 $t$ 输入到训练好的噪声预测网络 $\epsilon_{\theta}$,得到预测的噪声 $\epsilon_{\theta}(x_t, t)$。
b. 使用 $x_t$ 和预测出的噪声 $\epsilon_{\theta}(x_t, t)$,通过以下公式计算出上一个时间步 $x_{t-1}$(即一个噪声少一点的图像)。
c. 采样公式:
$$
x_{t-1}=\frac{1}{\sqrt{\alpha_{t}}}(x_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\overline{\alpha}{t}}}\epsilon{\theta}(x_{t},t))+\sigma_{t}z
$$
(其中 $z$ 是一个在 $t>1$ 时采样的标准高斯噪声,在 $t=1$ 时 $z=0$)当循环在 $t=1$ 结束时,得到的 $x_0$ 就是最终生成的清晰图像。
3. 核心数学原理
为什么是预测噪声?
这是整个 DDPM 数学推导的精华所在。
最终目标: 我们的目标是训练一个模型 $P_{\theta}(x_{t-1}|x_t)$ 来拟合真实的反向过程 $q(x_{t-1}|x_t, x_0)$。
目标均值: 通过数学推导(贝叶斯公式),可以证明 $q(x_{t-1}|x_t, x_0)$ 是一个高斯分布,其均值(Mean)为:
$$
\frac{\sqrt{\overline{\alpha}{t-1}}\beta{t}x_{0}+\sqrt{\alpha_{t}}(1-\overline{\alpha}{t-1})x{t}}{1-\overline{\alpha}_{t}}
$$问题: 这个均值依赖 $x_0$。在训练时我们可以拿到 $x_0$,但在采样(Inference)时,我们并没有 $x_0$($x_0$ 是我们要生成的目标)。
关键洞察(重参数化): 我们有前向过程的“捷径”公式:
$$
x_{t}=\sqrt{\overline{\alpha}{t}}x{0}+\sqrt{1-\overline{\alpha}{t}}\epsilon
$$
我们可以用它来反解 $x_0$:
$$
x{0} = \frac{x_{t}-\sqrt{1-\overline{\alpha}{t}}\epsilon}{\sqrt{\overline{\alpha}{t}}}
$$代换: 将这个 $x_0$ 的表达式代入到步骤 2 中的均值公式中,经过一系列化简,可以得到一个等价的均值表达式:
$$
\frac{1}{\sqrt{\alpha_{t}}}(x_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\overline{\alpha}_{t}}}\epsilon)
$$结论:
这个新的均值公式**只依赖 $x_t$ 和 $\epsilon$**,不再依赖 $x_0$,$x_t$ 是我们已知的(网络的输入)。
这意味着,我们的神经网络 $P_{\theta}$ **只需要预测 $\epsilon$,就可以计算出这个目标均值。这就是为什么 DDPM 的神经网络被设计为噪声预测器 $\epsilon_{\theta}$**。
这也解释了算法 2(采样)中的公式是如何来的。
为什么采样时需要添加随机噪声 $\sigma_t z$?
在算法 2 的采样公式中,除了通过 $\epsilon_{\theta}$ 计算出的均值(确定性部分),还多了一项 $\sigma_t z$(随机性部分)。
PPT 提问:为什么不直接取均值,而是要进行“采样”?
猜想(类比文本生成):
在文本生成任务中,如果总是选择概率最高的词(如 Beam Search),会很快陷入重复、无意义的循环(称为 “Neural Text Degeneration”)。
相反,使用“采样”(Sampling)会引入随机性,使得生成的文本更具多样性、更像人类的表达。
Diffusion Model 也是一个自回归(Autoregressive)的过程,它在 $T$ 步中逐步生成结果。在每一步去噪时都添加一点随机噪声,可以防止模型“卡住”,并极大丰富生成结果的多样性。
4. 扩展应用:离散数据(如文本)
困难点: 文本是离散的(”你好吗?”),无法直接对其施加高斯噪声。
解决方案:
在隐空间 (Latent Space) 加噪: 不对离散的 token 加噪,而是对它们的连续表示(如 Word Vectors 或 Embeddings)加高斯噪声 (如 Diffusion-LM, DiffuSeq)。
使用非高斯噪声: 将“加噪”过程替换为更适合离散数据的“损坏”过程,例如“随机 Masking”或“词语替换”,然后训练模型重建原始文本(如 DiffusER, MaskGIT)。这使得 Diffusion 的思想与 Masked Autoencoder(如 BERT)产生了联系。